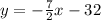Given:
There are given that the slope and the point:
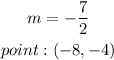
Step-by-step explanation:
To find the equation, first, we need to see the formula for slope-intercept form:
So,
From the slope-intercept formula;

Where,
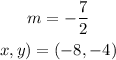
Now,
We need to find the value of b by using given information:
So,
Put all the given values into the given slope-intercept form:
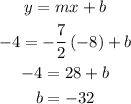
Then,
Put the value of b and m into the slope-intercept form;
So,
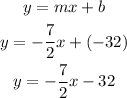
Final answer:
Hence, the equation of a line is shown below;