Question

Which answers are geometric sequences?There is more than one correct answer. Select all that apply.a. {2, -10,50,- 250, ...}b. {1,-1,1,-1,1,...}c. {0, 10, 20, 30,...}d. (2.5,4,5.5, 7,...)e. {-13, -6, 1,8,...)f. (108, 36, 12, 4,...)

Answer 1

Given:

The objective is to choose the correct geometric sequence all that apply.

Geometric ratio is defined as the sequence of series containing equal ratio for successive terms.

`r=(a_2)/(a_1)=(a_3)/(a_2)=(a_4)/(a_3)`

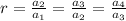
Consider option (a), (2, -10, 50, -250, .......).

Here, a1 = 2, a2 = -10, a3 = 50 and a4 = -250

Then the common ratio will be,

`\begin{gathered} r=(-10)/(2)=(50)/(-10)=(-250)/(50) \\ r=-5 \end{gathered}`

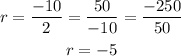
Thus, option (a) is a geometric sequence.

Consider option (b) (1, -1, 1, -1, 1...)

Here, a1 = 1, a2 = -1, a3 = 1, a4 = -1.

Then the common ratio will be,

`\begin{gathered} r=(-1)/(1)=(1)/(-1)=(-1)/(1) \\ r=-1 \end{gathered}`

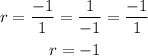
Thus, option (b) is a geometric sequence.

Consider option (c) (0, 10, 20, 30....)

Here, a1 = 0, a2 = 10, a3 = 20, a4 = 30............

Then, the common ratio will be,

`\begin{gathered} r=(10)/(0)=(20)/(10)=(30)/(20) \\ r=\infty\\e2\\e1.5 \end{gathered}`

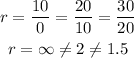
Thus, option (c) is not a geometric sequence.

Consider option (d) (2.5, 4, 5.5, 7....)

Here, a1 = 2.5, a2 = 4, a3 =5.5 and a4 = 7.

Then, the common ratio will be,

`\begin{gathered} r=(4)/(2.5)=(5.5)/(4)=(7)/(5.5) \\ r=1.6\\e1.3\\e1.27 \end{gathered}`

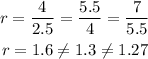
Thus, option (d) is not a geometric sequence.

Consider option (e) (-13, -6, 1, 8....)

Here, a1 = -13, a2 = -6, a3=1 and a4 = 8.

Then, the common ratio will be,

`\begin{gathered} r=(-6)/(-13)=(1)/(-6)=(8)/(1) \\ r=0.4\\e-0.16\\e8 \end{gathered}`

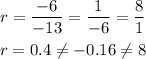
Thus, option (e) is not a geometric sequence.

Consider option (f), (108, 36, 12, 4...)

Here, a1 = 108, a2 = 36, a3 = 12 and a4 = 4.

Then, the common ratio will be,

`\begin{gathered} r=(36)/(108)=(12)/(36)=(4)/(12) \\ r=(1)/(3)=(1)/(3)=(1)/(3) \end{gathered}`

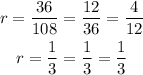
Thus, option (f) is a geometric sequence.

Hence, the correct geometric sequences are option (a), (b) and (f).