Question

A stone is thrown into a pond. A circular ripple is spreading over the pond in such a way that the radius is increasing at the rate of 6.4 feet per second. Find a function, r(t), for theradius in terms oft. Find a function, A(r), for the area of the ripple in terms of r. Find (A or) (t).

Answer 1

From the question, the r is increasing at the rate of 6.4 feet per seconds.

This means that the equation of the radius is

`r=6.4* t`

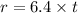
So the function for the radius, in terms of t becomes

`r(t)=6.4t`

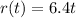
The Area A is given as

`A=\pi r^2`

So, the function for the area in terms of r becomes

`A(r)=\pi r^2`

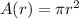
Now, (A . r)t becomes

`\begin{gathered} (A.r)t=\pi r^2,\text{ where r\lparen t\rparen = 6.4t, we have } \\ (A.r)t=\pi*(6.4t)^2 \\ =40.96\pi t^2 \end{gathered}`

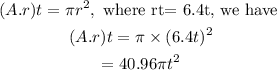
Hence the answer is

`(A.r)t=40.96\pi t^2`

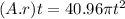
The 3rd option is the answer