Question

A scientist has two solutions, which she has labeled as Solution A and Solution B. Each contains salt. She knows that Solution A is 70% salt and Solution B is 95% salt. She wants to obtain 160 ounces of a mixture that is 85% salt. How many ounces of each solution should she use?

Answer 1

The Solution.

Let the amount of solution A in the mixture be represented with x.

So, we have the equation below:

(70% of x) + 95%(160 -x) = 85% of 160

`0.7x+0.95\mleft(160-x\mright)=0.85\mleft(160\mright)`

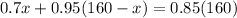
Clearing the brackets, we get

`0.7x+152-0.95x=136`

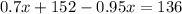
Collecting the like terms, we get

`\begin{gathered} 0.7x-0.95x=136-152_{} \\ -0.25x=-16 \end{gathered}`

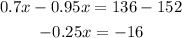
Dividing both sides by -0.25, we get

`x=(-16)/(-0.25)=64\text{ ounces}`

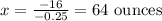
So, solution A is 64 ounces.

While that of solution B is

`160-64=96\text{ ounces}`

Hence, the correct answer is:

solution A is 64 ounces while solution B is 96 ounces.