Question

Summer SwimmingPart C120Graph your two equations from Part Aand Part B.110100Total Cost80GraphingTools604020246810 12 14ONumber of Days

Answer 1

We are required to graph out the equations from A and B.

In order to graph out the equations, we need a table of values for our x and y axes.

We can choose the values for our x-axis to be from 0 to 14 moving in steps of 2.

While there will be two corresponding y-values. One for y = 7x and the other for y = 30 + 4x

Therefore, we need to calculate these y values which we shall denote y1 and y2 respectively.

This is done below:

`\begin{gathered} \text{when x = 0;} \\ y_1=7*0=0 \\ y_2=30+4(0)=30 \\ \\ \text{when x = 2;} \\ y_1=7*2=14 \\ y_2=30+4(2)=38 \\ \\ when\text{ x = 4;} \\ y_1=7*4=28 \\ y_2=30+4(4)=46 \\ \\ \text{when x= 6;} \\ y_1=7*6=42 \\ y_2=30+4(6)=54 \\ \\ \text{when x = 8;} \\ y_1=7*8=56 \\ y_2=30+4(8)=62 \\ \\ \text{when x= 10;} \\ y_1=7*10=70 \\ y_2=30+4(10)=70 \\ \\ \text{when x= 12;} \\ y_1=7*12=84 \\ y_2=30+4(12)=78 \\ \\ \text{when x = 14;} \\ y_1=7*14=98 \\ y_2=30+4(14)=86 \end{gathered}`

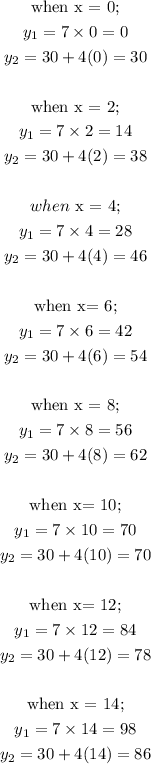
The calculated coordinates are:

(x, y1), (x, y2):

(0, 0), (0, 30)

(2, 14)(2, 38)

(4, 28)(2, 46)

(6, 42)(6, 54)

(8, 56)(8, 62)

(10, 70)(10, 70)

(12, 84)(12, 78)

(14, 98)(14, 86)

Now that we have calculated the values of the coordinates, we can create the table:

Now that we have the table of values, we can now plot the values:

The x values on the x-axis and the y-values on the y-axis

A picture of the plot is shown below:

Notice that on the table of values, both y1 and y2 have the same y-value at x = 10. This is the same point in which the graphs of y1 and y2 intersect i.e. at point x = 10, y = 70