It is required to factor the given polynomial by completing the table.
The given polynomial is:
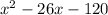
Add the factors listed in the table to complete the table as follows:
Notice that only the sum of the factors 4 and -30 gives the coefficient of x, -26.
Hence, write -26x as -30x+4x to factorize the polynomial as follows:
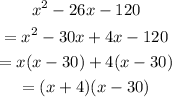
The answer is (x+4)(x-30).