Question

Find the zeros of each function by factoring. f(x)=x^2+2x–35

Answer 1

Finding the zeros of a function means finding the values that make "f(x) = 0".

`\begin{gathered} f(x)=x^2+2x-35 \\ 0=x^2+2x-35 \end{gathered}`

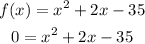
We need to find the factors of "-35" that when added are equal to "2".

`\begin{gathered} -35=7\cdot-5 \\ -35=-7\cdot5 \end{gathered}`

There are only two pairs of factors for "-35", its either "7" and "-5" or "-7" and "5". When added the only one that results in "2" is the first. So we can rewrite the expression as:

`0=(x+7)(x-5)`

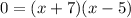
And the zeros of the function happen when either of these terms is equal to 0, so we have:

`\begin{gathered} x+7=0_{} \\ x=-7 \\ x-5=0 \\ x=5 \end{gathered}`

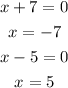
The two zeros are 5 and -7.