Question

What is the position vector of the midpoint of the line PQ if P has coordinates(-6,4,2) and Q has coordinates (10,8,12)?A. (2,-6,7)B. (2,6,7)OC. (-2,6,-7)D. (-2,-6,-7)

Answer 1

To obtain the position vector of the midpoint of the line PQ, the following steps are necessary:

Step 1: Recall the expression for the line AB, obtained from two position vectors A, and B, as follows:

`\vec{AB}=\vec{B}-\vec{A}`

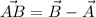
Also:

`\begin{gathered} \text{If:} \\ \vec{A}=(a_1,a_2,a_3) \\ \vec{B}=(b_1,b_2,b_3) \\ \text{Thus:} \\ \vec{AB}=\vec{B}-\vec{A}=(b_1,b_2,b_3)-(a_1,a_2,a_3)=(b_1-a_1,b_2-a_2,b_3-a_3) \end{gathered}`

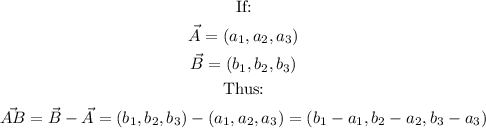
Step 2: Recall the expression for the midpoint of the line vector PQ, as given below:

`\begin{gathered} \text{midpoint}=\vec{P}+(1)/(2)\vec{PQ} \\ \Rightarrow\text{midpoint}=\vec{P}+(1)/(2)(\vec{Q}-\vec{P})=\vec{P}+(1)/(2)\vec{Q}-(1)/(2)\vec{P}=(1)/(2)\vec{Q}+(1)/(2)\vec{P} \\ \Rightarrow\text{midpoint}=(1)/(2)(\vec{Q}+\vec{P}) \end{gathered}`

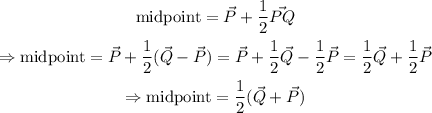
Thus:

`\begin{gathered} \text{If:} \\ \vec{P}=(p_1,p_2,p_3) \\ \vec{Q}=(q_1,q_2,q_3) \\ \text{Thus:} \\ \Rightarrow\text{midpoint}=(1)/(2)(\vec{Q}+\vec{P}) \\ \Rightarrow\text{midpoint}=(1)/(2)((q_1,q_2,q_3)+(p_1,p_2,p_3))=(1)/(2)(q_1+p_1,q_2+p_2,q_3+p_3) \end{gathered}`

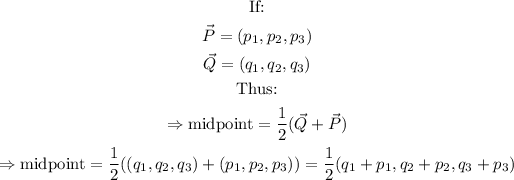
Step 3: Apply the formula for the midpoint of line PQ, to the question, as follows:

`\begin{gathered} \text{Given that:} \\ \vec{P}=(-6,4,2) \\ \vec{Q}=(10,8,12) \\ \text{Thus:} \\ \Rightarrow\text{midpoint}=(1)/(2)(q_1+p_1,q_2+p_2,q_3+p_3) \\ \Rightarrow\text{midpoint}=(1)/(2)(-6+10,4+8,2+12)=(1)/(2)(4,12,14)=(2,6,7) \\ \Rightarrow\text{midpoint}=(2,6,7) \end{gathered}`

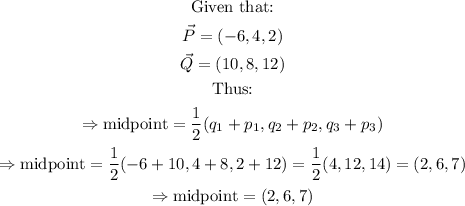
Therefore, the position vector of the midpoint of the line PQ is : (2, 6, 7) (option B)