We will investigate the application of pythagorean theorem for right angle triangles.
A right angle triangle is denoted by one of its interior angle as 90 degrees. It has three side lengths denoted as follows:

The pythagorean theorem relates the longest length of a right angle triangle ( H ) - hypotenuse with the other two side lengths of a right angle triangle by the following expression:
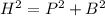
Lets say we have three side lengths of a triangle given as follows:
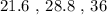
For the triangle with above denoted side lengths to be classified as a " right angle triangle" then it needs to conform to the pythagorean theorem states above. We will check whether the side lengths follows the pythagorean theorem or not.
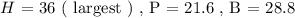
Using pythagorean theorem:
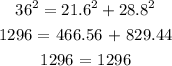
Since the right hand side equals the left hand side the pythagorean theorem is validated. This also means that the given triangle is a right angled triangle! Hence,