16 ft
Step-by-step explanation
Step 1
because the ligth comes in the same angle, we have 2 similar triangles .
so,as the triangles are similar,the ratio of the shorter leg to the bigger leg must be equal.
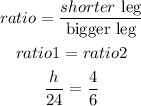
Step 2
solve for h

therefore, the heigth of the tree is 16 ft