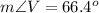Question

Leaming Diagnostic Analytics Recommendations Spans Me AS Trigonometric ratios find an angle measures You have Find m2V v 2 U 5 W write your answer as an integer or as a decimal rounded to the nearest tenth. m2 = 1

Answer 1

Given:

The triangle VUW is the right-angled triangle.

`VU=2\text{ and VW=5.}`

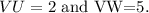
Required:

`\text{ We need to find m}\angle V.`

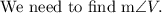
Step-by-step explanation:

The adjacent side of the angle V is VU=2.

The hypotenuse of the triangle is VW=5.

Use the cosine formula.

`cos(m\angle V)=\frac{Adjacent\text{ side}}{Hypotenuse}`

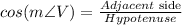
Substitute the adjacent side =2, and the hypotenuse = VW=5 in the formula.

`cos(m\angle V)=(2)/(5)`

`cos(m\angle V)=0.4`

`m\angle V=cos^(-1)(0.4)`

`m\angle V=66.4^o`

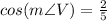
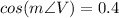
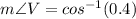
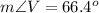
Final answer:

`m\angle V=66.4^o`