Answer:
The area of the triangle is 31.3
Step-by-step explanation:
Here, we want to get the area of the triangle
We start by calculating the length of the missing side
We can find this by the use of the Cosine rule
Mathematically,we have this as:
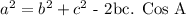
We proceed to substitute the values as follows:
![\begin{gathered} a^2=10^2+9^2\text{ -2(10)(9) Cos 44} \\ a^2\text{ = 51.52} \\ a=\sqrt[]{51.52} \\ a\text{ = 7.2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/pg77rp9g7t61zariz87hpdt08e49vi8i5e.png)
Since we have the third side, we can use Heron's formula to get the area of the triangle as follows:
![\begin{gathered} A\text{ = }\sqrt[]{s(s-a)(s-b)(s-c)} \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/3sms0nxh4htr79bp35hrdc0kog9m2nt3gi.png)
Where s represents the semi-perimeter which can be calculated as:
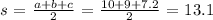
Finally, we can compute the area of the triangle as follows:
![\begin{gathered} A\text{ = }\sqrt[]{13.1(13.1-10)(13.1-9)(13.1-7.2)} \\ A\text{ =}\sqrt[]{13.1*3.1*4.1*5.9} \\ A\text{ = }\sqrt[]{982.3559} \\ A\text{ = 31.3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/x62qbzr9gitqhsoy9mjfn0tf8tng1p49b1.png)