Question

Determine whether AB and MN are parallel, perpendicular, or neither. 7. A(0, 3), B(5, -7), M(-6, 7), N(-2,-1)

Answer 1

7. AB and MN are parallel lines

Step-by-step explanation:

Two lines are parallel if they have the same slope and two lines are perpendicular if the product of their slopes is equal to -1.

So, to find the slope m of a line we can use the following equation:

`m=(y_2-y_1)/(x_2-x_1)`

Where (x1, y1) and (x2, y1) are two points in the line.

So, the slope of AB is calculated replacing (x1, y1) by A(0,3) and (x2, y2) by (5, -7). Then:

`m=(-7-3)/(5-0)=-(10)/(5)=-2`

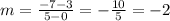
In the same way, the slope of MN is calculated replacing (x1, y1) by M(-6, 7) and (x2, y2) by (-2,-1). So:

`m=(-1-7)/(-2-(-6))=(-8)/(-2+6)=(-8)/(4)=-2`

Since the slopes of AB and MN are both equal to -2, AB and MN are parallel lines.