We have a initial population P(0) of 3800.
We know that the population is decreasing by 1.4% each year, so the population at year 1 (2009) we will have a population of:
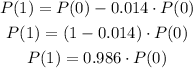
We can generalize this for P(n), where n is the number of years from 2008.
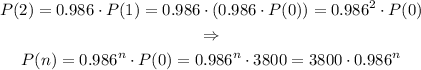
From 2008 to 2013 we have 2013-2008=5 years, so for the year 2013, the value of n is n=5.
Then, the population for 2013 will be P(5) and can be calculated as:
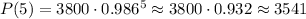
Answer: the predicted population for the year 2013 is 3541.