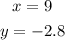Question

Solve the following system of equations without graphing: 4x + 5y = 22 4x + 10y = 8 Write your solution as an ordered pair ) (Remember: you want to eliminate one of the variables)

Answer 1

The system of equations we have is:

`\begin{gathered} 4x+5y=22 \\ 4x+10y=8 \end{gathered}`

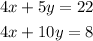
Step 1. substract the second equation from the first equation to eliminate variable x:

`\begin{gathered} 4x+5y=22 \\ -(4x+10y=8) \end{gathered}`

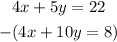
The minus sign changes the signs of the second equation, and now we have:

`\begin{gathered} 4x+5y=22 \\ -4x-10y=-8 \end{gathered}`

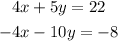
and the result of this is:

Step 2. From the result of the substraction -5y=14, solve for y:

`\begin{gathered} -5y=14 \\ y=(14)/(-5) \\ y=-2.8 \end{gathered}`

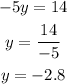
Step 3. Substitute this value of y in the first original equation

`4x+5y=22`

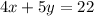
To find the value of x.

We substitute y=-2.8

`4x+5(-2.8)=22`

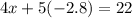
Step 4. Solve for x

`\begin{gathered} 4x-14=22 \\ 4x=22+14 \\ 4x=36 \\ x=(36)/(4) \\ x=9 \end{gathered}`

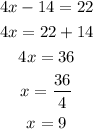
Answer:

`\begin{gathered} x=9 \\ y=-2.8 \end{gathered}`