Let x be the distance traveled by one of the buses (let's call it Bus A) and y be the rate of the other bus (let's call it Bus B).
Let's remember the relation that exist between the speed (rate), the distance and the time:
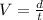
We know that it takes 3 hours for Bus A to travel x miles at a speed of y+15 (it is 15 faster than Bus B). This expressed as an equation is:

We also know that it takes 3 hours for Bus B to travel 405-x miles at a speed of y:
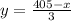
Solve the obtained system of equations by equalization:
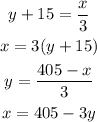
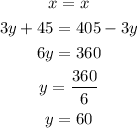
The rate of Bus B is 60 and the rate of Bus A is 75 (Bus A is 15 faster than Bus B).