Question

A line that passes through the point (-1,3) has a slope of 2.find another point on the line.Options:A :(1,4) b (-3,2) c (1,5) d (0,5)

Answer 1

Lets find the equation of the line. The equation of the line that passes through a point is:

`y-y_0=m(x-x_0)`

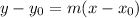
where x_0 and y_0 are the coordinates of the point and m is the slope.

Then, in this case m = 2 and the point (-1, 3)

We can write:

`y-3=2(x-(-1))`

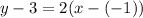
And solve for y:

`\begin{gathered} y=2x+2+3 \\ \end{gathered}`

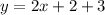
The equation of the line is:

`y=2x+5`

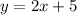
Now to see which of the options is a point in the line, we evaluate each x coordinate to see if give us the correct y coordinate.

The option a is (1, 4)

`\begin{gathered} y=2\cdot1+5 \\ y=7 \end{gathered}`

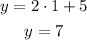
Option a cannot be.

Option b is (-3, 2)

`\begin{gathered} y=2\cdot(-3)+5 \\ y=-6+5 \\ y=-1 \end{gathered}`

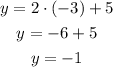
Option b cannot be either

Option c is (1, 5) but we already know that the y coordinate when x = 1 is 7. C cannot be.

Finally, option D is (0, 5)

`\begin{gathered} y=2\cdot0+5 \\ y=5 \end{gathered}`

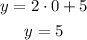
Wich is correct.

Thus, the correct answer is option D.