Question

Spongebob Squarepants is helping Mr.Krabs place an order for the Krusty Krab. Spongebob has decided to order cod (which is $3 a pound) and salmon (which is $8 a pound). He needs to buy at least 40 pounds of fish, but Mr.Krabs is a cheapskate and has told he can spend a maximum of $240. a) Write a system of inequalities that models this situation. Then graph your system. Be sure to define your variables and label each axis.b.) spongebob wants to order 60 pounds of cod and 5 pounds of salmon. Explain how the graph shows whether he can do this or not.

Answer 1

We are given a problem that can be solved using inequations. First, let's define the following variables:

`\begin{gathered} x=\text{ pounds of cods} \\ y=\text{ pounds of salmons} \end{gathered}`

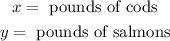
We are told that there must be at least 40 pounds of fish, that means that the sum of the pounds of cods and the pounds of salmons must be greater than 40, this can be written mathematically as:

`x+y\ge40`

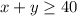
We are also told that the total cost must not surpass $240. We know the cost per pound of cods and salmons, that means that the product of the cost per pound and the pounds of each fish must be smaller than 240, this can be written mathematically like this:

`3x+8y\le240`

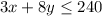
Therefore, the system of inequalities is:

`\begin{gathered} x+y\ge40,\text{ (1)} \\ 3x+8y\le240,\text{ (2)} \end{gathered}`

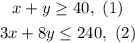
The graph of this system is the following:

The intersection between the two colors is the solution for the system of equations.

for part (b), we are asked wheater 60 pounds of cod and 5 pounds of salmon is allowed. This equivalent to asking if the point (x,y) = (60,5) is one of the solutions to the system of equations. To determine that analytically, we replace the values of x and y in each of the equations of the system. Replacing in equation (1) we get:

`\begin{gathered} x+y\ge40 \\ 60+5\ge40 \\ 65\ge40 \end{gathered}`

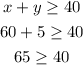
Since we get a true value, that is 65 is bigger than 40, the solution is true for equation (1). Now we replace in equation (2):

`\begin{gathered} 3x+8y\le240 \\ 3(60)+8(5)\le240 \\ 180+40\le240 \\ 220\le240 \end{gathered}`

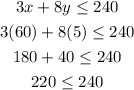
Since 220 is smaller than 240 this is a solution for equation (2). Since it is a solution for both equations, the point is a solution for the system. Graphically this can be seen for the fact that the point (60,5) lies in the intersection between the two colors of the graph like we can see next: