1 Answer

JoRouss · Answer 1 · 2023-05-28T06:36:59+0000

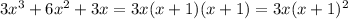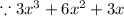
$\because3x^3+6x^2+3x$

→ To factorize it we must find the greatest common factor of the 3 terms

∵ The common factor of 3, 6, and 3 is 3

∵ The common factor of x^3, x^2, and x is x

∴ The greatest common factor of the 3 terms is 3x

→ Divide each term by 3x

$\because(3x^3)/(3x)=x^2$
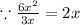
$\because(6x^2)/(3x)=2x$
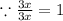
$\because(3x)/(3x)=1$

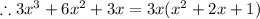
$\therefore3x^3+6x^2+3x=3x(x^2+2x+1)$

→ Now we must factorize the bracket into two factors

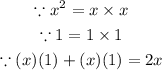
$\begin{gathered} \because x^2=x* x \\ \because1=1*1 \\ \because(x)(1)+(x)(1)=2x \end{gathered}$
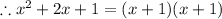
$\therefore x^2+2x+1=(x+1)(x+1)$

∴ The complete factorization is

Please log in or register to add a comment.