Answer:
16
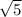 +4
+4
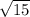 or 51.26902
or 51.26902
Explanation:
Consider one of the smaller, right-angled triangles within the main triangle, and use sine to find the hypotenuse of the small triangles:
sinA=opposite/hypotenuse
sin60=4
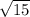 /hypotenuse
/hypotenuse
hypotenuse=
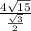
hypotenuse=8(
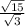 )
)
hypotenuse=8
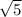
So the left and right hand sides of the larger triangle are both 8
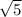 respectively.
respectively.
To find the base, once again consider the smaller triangle, and this time, use pythagorus:
a²=b²+c²
(8
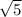 )²=(4
)²=(4
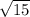 )²+c²
)²+c²
320=240+c²
80=c²
c=4
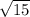
So the perimeter is 8
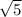 +8
+8
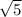 +4
+4
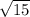 =16
=16
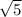 +4
+4
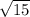 =51.26902
=51.26902