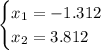Given the following function:
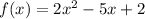
We want to know the 'x' values for
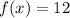
If we define
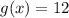
We want the interception between f(x) and g(x). Plotting both of them, we get the following:
Where the red parabola is the f(x) function, and the blue line is the g(x) function.
If you graph them, you're going to find out that the interception are in the points:
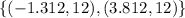
Then, our x values are: