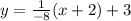Question

If f(3)=-2, f’(3)=-8, and g(x) is the inverse function to f(x), the equation of the tangent line to g(x) at x=-2 is

Answer 1

Given:

`\begin{gathered} f(3)=-2 \\ f^{^(\prime)}(3)=-8 \\ g(x)=(1)/(f(x)) \end{gathered}`

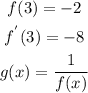
Solution:

If f(3)=-2, then f'(-2)=3

Hence, the points are (-2,3). These points will be on the graph of the inverse function to f(x).

The function g(x) is as

`\begin{gathered} g(x)=y \\ =(1)/(f(x)) \end{gathered}`

Now, the tangent line slop will be as

`\begin{gathered} f(-2)=\frac{1}{f^{^(\prime)}(3)} \\ =(1)/(-8) \end{gathered}`

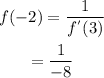
The equation of the tangent line will be as

`\begin{gathered} y-3=(1)/(-8)(x-(-2)) \\ y-3=(1)/(-8)(x+2) \end{gathered}`

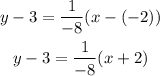
Answer:

Hence, the tangent line equation is as

`y=(1)/(-8)(x+2)+3`