Answer:
-2 - i
Step-by-step explanation:
When the polynomial has a zero with the form a + bi, it also has a zero with the form a - bi. So, the fourth zero of the polynomial should be:
-2 - i
And we can prove that it is a zero replacing x by (-2 - i) on the initial equation as:
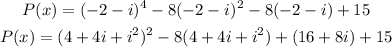
Where i²= -1, so P(x) is:
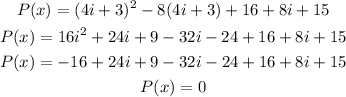
Therefore, the fourth zero is:
-2 - i