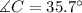Question

If the measure of angle A= 55degrees, b= 12, and C=7, thenfind the measure of angle C.

Answer 1

The measure of angle C is;

`\measuredangle C=35.7^(\circ)`

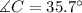
Step-by-step explanation:

Given the figure in the attached image.

To get angle C, we will need to first calculate the length of side a.

Applying cosine rule;

`a=\sqrt[]{b^2+c^2-2bc\cos A}`

given;

`\begin{gathered} b=12 \\ c=7 \\ A=55^(\circ) \end{gathered}`

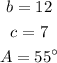
substituting the given values;

`\begin{gathered} a=\sqrt[]{12^2+7^2-2(12)(7)\cos 55} \\ a=9.83 \end{gathered}`

We can now solve for angle C;

`\begin{gathered} \cos C=(a^2+b^2-c^2)/(2ab) \\ \text{substituting;} \\ \cos C=(9.83^2+12^2-7^2)/(2(9.83)(12)) \\ \cos C=0.81226 \\ C=\cos ^(-1)(0.81226) \\ C=35.7^(\circ) \end{gathered}`

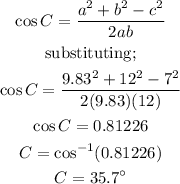
Therefore, the measure of angle C is;

`\measuredangle C=35.7^(\circ)`