Question

I need help with 19, 20, 21, and 22 please

Answer 1

We can calculate the line equation with two points the following manner:

`\begin{gathered} P_1=(x_1,y_1),P_2=(x_2,y_2) \\ \text{The slope m is:} \\ m=(y_2-y_1)/(x_2-x_1) \\ \text{And the line equation in the point-slope equation is:} \\ y-y_1=m\cdot(x-x_1) \end{gathered}`

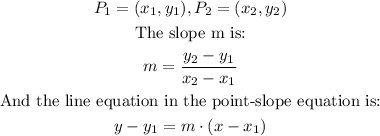
For problem 19, we have:

`\begin{gathered} P_1=(2,-2),P_2=(5,7) \\ The\text{ slope is:} \\ m=(7-(-2))/(5-2)=(7+2)/(3)=(9)/(3)=3 \\ \text{The point-slope form is:} \\ y-(-2)=3\cdot(x-2) \\ y+2=3(x-2) \end{gathered}`

For problem 20, we have:

`\begin{gathered} P_1=(6,4),P_2=(2,1) \\ \text{The slope is:} \\ m=(1-4)/(2-6)=((-3))/((-4))=(3)/(4) \\ \text{The point-slope form is:} \\ y-4=(3)/(4)(x-6) \end{gathered}`

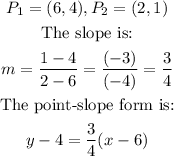
For problem 21 and 22, we have to graph the equations, to do that we need to find two points on the line.

For problem 21, we can choose x = 2 and x = 3 and found the respective y-value:

`\begin{gathered} \text{The equation is:} \\ y-1=2(x-4) \\ \text{For x = 2,} \\ y-1=2(2-4)=2\cdot(-2)=-4 \\ y=-4+1=-3 \\ So,\text{ the first point is (2, -3)} \\ \text{For x = 3,} \\ y-1=2(3-4)=2\cdot(-1)=-2 \\ y=-2+1=-1 \\ So,\text{ the second point is (3, -1)} \end{gathered}`

With the points (2, -3) and (3, -1) we can graph the line: