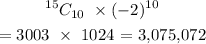Question

12) What is the constant in the expansion of (x^2 - 2/x)^15, if it exists?

Answer 1

The constant term in the expansion is:

`3,075,072`

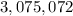
Step-by-step explanation:

Here, we want to get the constant term in the polynomial expansion

For us to get the constant term in the expansion, we have to understand that the term x^2 and the term 2/x must be similar in terms of the power of x to have canceled out

At any term in the expasnion, the power of x^2 and the 2/x power must be summed to be equal to 15

Mathematically, if we have the expansion as follows:

`+\ldots..+^(15)C_(10)(x^2)^5(-(2)/(x))^(10)\text{ + }\ldots\ldots`

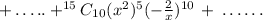
If we expanded this, we will have the x^10 canceling out 1/x^10

Thus, we have the constant term as:

`\begin{gathered} ^(15)C_(10)\text{ }*(-2)^(10) \\ =3003\text{ }*\text{ 1024 = 3,075,072} \end{gathered}`