Question

The following equation has four solutions: x^4+6x^2=-8The two imaginary solutions with rational coefficients are +__i and two imaginary solutions with irrational coefficients are +I✔️(__).

Answer 1

Given

The equation,

`x^4+6x^2=-8`

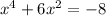
To find:

The roots of the given equation.

Step-by-step explanation:

It is given that,

`x^4+6x^2=-8`

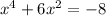
That implies,

`\begin{gathered} x^4+6x^2=-8 \\ x^4+6x^2+8=0 \end{gathered}`

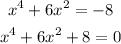
Put x²=y.

Then,

`\begin{gathered} y^2+6y+8=0 \\ y=(-6\pm√(36-32))/(2) \\ y=(-6\pm√(4))/(2) \\ y=(-6\pm2)/(2) \\ y=(-6+2)/(2),\text{ }y=(-6-2)/(2) \\ y=(-4)/(2),\text{ }y=(-8)/(2) \\ y=-2,\text{ }y=-4 \end{gathered}`

Therefore,x

`\begin{gathered} x^2=-2,\text{ }x^2=-4 \\ x=\pm√(-2),\text{ }x=\pm√(-4) \\ x=\pm i√(2),\text{ }x=\pm2i \end{gathered}`

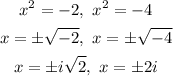
Hence, the two imaginary ssolutions with rational coefficients are ±2i, and the two imaginary solutions with irrational coefficients are ±i√(2).