Question

Find the height of the can in inches. Round your answer to the nearest tenth if necessary.(Info in figure)

Answer 1

Given the model of the cylindrical can as shown below:

The circumference of the cylinder is

`4(1)/(2)\text{ inches}`

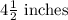
Volume of the cylinder is 7 cubic inches.

Required: Height of the can in inches

The circumference of the cylinder is expressed as the circumference of its circular cross-section.

Thus,

`\begin{gathered} \text{Circumference = 2}*\pi* r \\ \text{where} \\ r\Rightarrow radius\text{ of the circular cross-section} \end{gathered}`

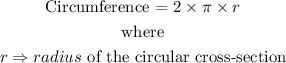
this gives

`\begin{gathered} 4(1)/(2)\text{ = 2}*\pi* r \\ (9)/(2)=2*\pi* r \\ \text{divide both sides by 2}\pi \\ \text{thus,} \\ r=(9)/(4\pi) \end{gathered}`

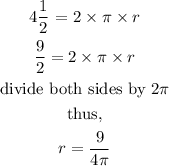
The volume of a cylinder is expressed as

`\begin{gathered} \text{Volume = }\pi* r^2* h \\ but\text{ r=}(9)/(4\pi) \\ \text{thus,} \\ 7\text{ = }\pi*((9)/(4\pi))^2* h \\ 7=\pi*(81)/(16\pi^2)* h \\ \Rightarrow h\text{ = }\frac{\text{16}\pi^2*7}{81\pi} \\ h\text{ = }4.34393 \end{gathered}`

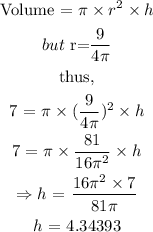
Hence, the height of the can in inches is 4.3 (nearest tenth).