According to the definition of the inverse function,
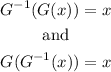
Therefore,
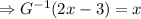
We need to construct G^-1(x) in such a way that when evaluated at 2x-3 the result is x.
Procedure:
1. Add +3 so that we transform 2x-3 into 2x
2. Multiply by 1/2 so that from 2x we get x
Algebraically,
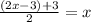
Then, G^-1(x) is

The answer is G^-1(x)=(x+3)/2