Question

system of equation solve a system of equations using elmination graph what the system of equations that you solved would look like

Answer 1

Let's take the system of equations:

• 2x + 3y = 15

,

• x - 3y = 3

Let's solve the system of equations using the elimination method.

To solve using the elimination method, let's first confirm the values of one variable are opposite.

Here, we can see the y variables are opposite, hence let's add both equations.

We have:

2x + 3y = 15

+ x - 3y = 3

____________

3x + 0 = 18

We now have:

3x = 18

Divide both sides by 3:

`\begin{gathered} (3x)/(3)=(18)/(3) \\ \\ x=6 \end{gathered}`

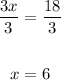
Plug in 6 for x in either of the equations and solve for y:

x - 3y = 3

6 - 3y = 3

Subtract 6 from both sides:

6 - 6 - 3y = 3 - 6

-3y = -3

Divide both sides by -3

`\begin{gathered} (-3y)/(-3)=(-3)/(-3) \\ \\ y=1 \end{gathered}`

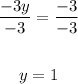
Therefore, the solution is:

x = 6, y = 1

Now, let's graph both equations.

Rewrite both equations in slope intercept form:

y = mx + b

We have:

Equation 1:

2x + 3y = 15

3y = -2x + 15

Divide all terms by 3

`\begin{gathered} (3y)/(3)=-(2x)/(3)+(15)/(3) \\ \\ y=-(2)/(3)x+5 \\ \end{gathered}`

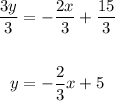
Equation 2:

x - 3y = 3

-3y = -x + 3

y = 1/3x - 1

Therefore, both equations in slope intercept form are:

y = -2/3x + 5

y = 1/3x - 1

Find two points on each equation,

Equation 1:

`\begin{gathered} When\text{ x = 3: }-(2)/(3)*3+5=-2+5=3 \\ \\ When\text{ x = -3: }-(2)/(3)(-3)=2+5=7 \end{gathered}`

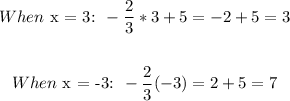
For equation 1, we have the points:

(x, y) ==> (3, 3) and (-3, 7)

Equation 2:

`\begin{gathered} When\text{ x =3: }y=(1)/(3)(3)-1=0 \\ \\ When\text{ x = -3: y}=(1)/(3)(-3)-1=-2 \end{gathered}`

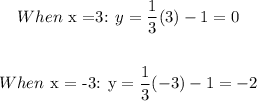
We have the points:

(x, y) ==> (3, 0) and (-3, -2)

Plot both points and connect them using a straight line.

We have the graph below:

We can see the graph of both equations above.

Both lines meet at the point: (6, 1)