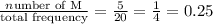Question

20 students were asked about their favorite college class the results are listed below let 8 equals astronomy be equal biology C equal chemistry M equal mathematic and E equal English

Answer 1

The Solution.

The frequency table of the given data is as below:

The data in the table above is QUANTITATIVE.

The relative frequency of the data above is calculated thus:

The relative frequency of Astronomy (A) is

`\frac{n\text{umber of A}}{\text{total frequency}}=(6)/(20)=(3)/(10)=0.3`

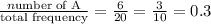
The relative frequency of Biology (B) is

`\frac{n\text{umber of B}}{\text{total frequency}}=(2)/(20)=(1)/(10)=0.1`

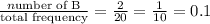
The relative frequency of Chemistry (C) is

`\frac{n\text{umber of C}}{\text{total frequency}}=(4)/(20)=(1)/(5)=0.2`

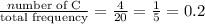
The relative frequency of Mathematics (M) is

`\frac{n\text{umber of M}}{\text{total frequency}}=(3)/(20)=0.15`

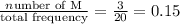
The relative frequency of English is

`\frac{n\text{umber of M}}{\text{total frequency}}=(5)/(20)=(1)/(4)=0.25`