Question

Find the length of the red line segment inside the cube.

Answer 1

Let's put more details in the figure to better understand the problem:

Given:

A = Side of the cube = 4 cm

B = Diagonal of the base = √(4² + 4²) = √(16 + 16) = √(32) = 4√2 cm

Connecting sides A, B and C, it appears to be a right triangle. Thus, to find C, we will be using the Pythagorean Theorem.

`\text{ C}^2=A^2+B^2`

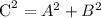
We get,

`\text{ C}^2=A^2+B^2\text{ }\rightarrow\text{ C = }\sqrt[]{A^2+B^2}`
`\text{C = }\sqrt[]{(4)^2+(4\sqrt[]{2})^2}`
`\text{ = }\sqrt[]{16\text{ + 16(2)}}\text{ }\rightarrow\text{ }\sqrt[]{16\text{ + 32}}`
`\text{ = }\sqrt[]{48}`
`=\text{ }\sqrt[]{\text{ 16 x 3}}\text{ = }\sqrt[]{16}\text{ x }\sqrt[]{3}`
`\text{ C = 4}\sqrt[]{3}`

Therefore, the measure of the red line segment is 4√3