Two lines are perpendicular if and only if their slopes fullfil:
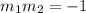
plugging the slope given we have:
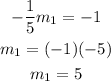
this means that the line we are looking for has slope 5.
Now, the slope of a line is given by:

we need to find two points that makes this slope equal to 5, choosing the points (1,4) and (2,9) we notice that:

Therefore the points we are looking for are (1,4) and (2,9)