Question

At Shake Shack in Center City, the delivery truck was unable to drop off the usualorder. The restaurant was stuck selling ONLY burgers and fries all Saturday long. 850items were sold on Saturday. Each burger was $5.79 and each order of fries was$2.99 for a grand total of $4.019.90 revenue on Saturday. How many burgers andhow many orders of fries were sold?

Answer 1

Let 'x' be the number of burgers sold and let 'y' be the number of orders of fries sold. Since 850 items were sold, we have that the first equation is:

`x+y=850`

next, we have that each burger costs $5.79 and each order of fries costs $2.99. Now, since the total revenue is $4019.90, then the second equation is:

`5.79x+2.99y=4019.90`

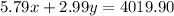
now, to solve this system of equations, we can solve for x the first equation to get the following:/

`x=850-y`

then, we can substitute this value on the second equation and solve for y to find the number of orders of fries:

`\begin{gathered} 5.79(850-y)+2.99y=4019.90 \\ \Rightarrow4921.50-5.79y+2.99y=4019.90 \\ \Rightarrow-2.8y=4019.90-4921.50=-901.6 \\ \Rightarrow y=(-901.6)/(-2.8)=322 \\ y=322 \end{gathered}`

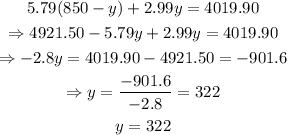
now that we have that y = 322, we can use this value on the first equation to find the value of x:

`x=850-322=528`

therefore, there were 528 burgers and 322 orders of fries sold