We have that the length measuring 2 feet more than twice the width so this means
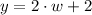
all in feet, now we know that the perimeter is 32 feet so we have
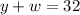
Using the first equation and replacing in the second one we get
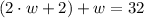
this is
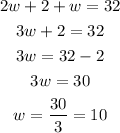
Replacing this in the first equation we get
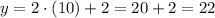
The answer is: the length of the garden is 22 and the width is 10 feet.