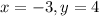
22) In order to make use of the Substitution Method, we need to rewrite one of those equations
7x+2y=-13
-3x-8y=23
22.1) So let's rewrite the first equation:
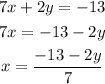
Now, we can plug this into the II equation.
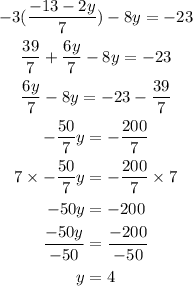
With this step, we could find the quantity of y. Let's plug into any equation, usually the simplest one (for convenience)
22.2)
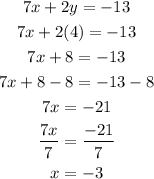
And then the answer is x=-3, y=4