From the conversion formula, given by
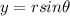
we have that
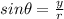
By substituting this result into the given polar equation, we have
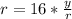
So, by multiplying both sides by r, we get
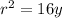
Now, from the conversion formula
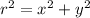
we have that
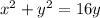
By subtracting 16y to both sides, we obtain

By completing the square of the quadratic equation on y, we get
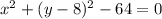
then, by adding 64 to both sides, we get
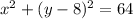
Therefore, the answer is the last option.