Question

what is the formula for the triangle below andfind the area of the triangle. Give the awnser to the nearest tenth

Answer 1

We can calculate the area of a triangle by means of the following formula:

`A=(b* h)/(2)`

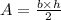
Where b is the length of the base and h is the height of the triangle.

The height of the triangle is a segment that goes from the top vertex to its base, like this:

As you can see in the above figure, the inscribed triangle on the right side is a right triangle, then we can apply the function sin(θ) in order to calculate the length of the side h, like this:

`\sin \theta=(h)/(a)`

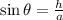
By replacing 70° for θ and 15 for a, we get:

`\begin{gathered} \sin (70)=(h)/(15) \\ (h)/(15)=\sin (70) \\ (h)/(15)*15=\sin (70)*15 \\ h*(15)/(15)=\sin (70)*15 \\ h*1=\sin (70)*15 \\ h=\sin (70)*15 \\ h=14.1 \end{gathered}`

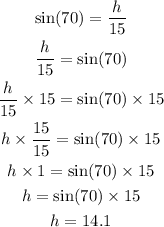
Now that we know the length of the side h, we can replace it into the formula of the area:

`A=(14.1*9)/(2)=63.4`

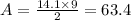
Then, the area of the triangle equals 63.4 square centimeters