Question

2. Consider the following equation with radicals and rational exponents. 11^19/4 • ^a√11^b = 11^9/4 • √11^3 What is the quotient of b and a?

Answer 1

The given expression :

`11^{(19)/(4)}\cdot\sqrt[a]{11^b}=11^{(9)/(4)}\cdot\sqrt[]{11^3}`

The exponents in the form of root can be express as :

`x^{(n)/(m)}=\sqrt[m]{x^n}`

So, the given expression simplify as :

`\begin{gathered} 11^{(19)/(4)}\cdot\sqrt[a]{11^b}=11^{(9)/(4)}\cdot\sqrt[]{11^3} \\ 11^{(19)/(4)}\cdot11^{(b)/(a)}=11^{(9)/(4)}\cdot11^{(3)/(2)} \end{gathered}`

Since the base of the exponents are same and the bases are multiply so, the exponents will sum up

`\begin{gathered} 11^{(19)/(4)}\cdot11^{(b)/(a)}=11^{(9)/(4)}\cdot11^{(3)/(2)} \\ 11^{(19)/(4)+(b)/(a)}=11^{(9)/(4)+(3)/(2)} \end{gathered}`

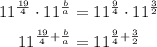
Now, the bases of exponents on both side are equal so, the exponents will equate together

`\begin{gathered} 11^{(19)/(4)+(b)/(a)}=11^{(9)/(4)+(3)/(2)} \\ (19)/(4)+(b)/(a)=(9)/(4)+(3)/(2) \\ (b)/(a)=(9)/(4)+(3)/(2)-(19)/(4) \\ (b)/(a)=(9+6-19)/(4) \\ (b)/(a)=(-4)/(4) \\ (b)/(a)=(-1) \\ b=(-1)a \\ \text{ From the divsion alogrithm } \\ \text{Dividend = Divisor}* Quotient+\text{ Remainder} \\ b=(-1)a \\ \text{Quotient of b =(-1)} \\ \text{Now, for a} \\ (b)/(a)=-1 \\ (b)/(a)=(-1)/(1) \\ \text{Apply cross multiplication} \\ b(1)=(-1)a \\ \text{Multiply by (-1)} \\ (-1)b=a \\ a=(-1)b \\ \text{From Division alogrithm} \\ \text{Quotient of a is (-1)} \end{gathered}`

Answer : Quotient of b and a is ( -1 ).