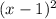Answer
Numerator:
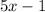
Denominator:
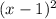
Step-by-step explanation
Problem Statement
The question asks us to simplify the complex rational expression given below:
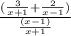
Solution
To solve the question, we will proceed to simplify the Numerator and Denominator separately.
Numerator:

Denominator:
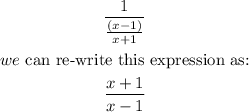
Now, let us combine the Numerator and Denominator as follows:
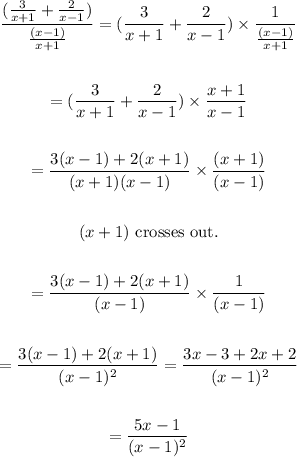
Final Answer
Numerator:
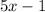
Denominator: