Given:
Invest amount = $5500
Rate = 9.10%
Time = 10 years
After that rate = 5%
Total time = 25 years
Find-:
The final amount after 25 years
Explanation-:
Future value is:
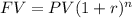
Where,

Amount after 10 years is:

The amount after 10 years is $13140.449
Amount after total years 25 then time for 5%

So, the amount is:
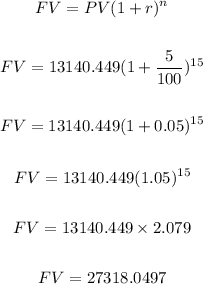
The total amount after 25 years is $273178.0497