Answer:
• (a)(i)1:200,000 (ii)16km
,
• (b)i)4:3 (ii)2.25mm, 3mm and 3.75mm.
Step-by-step explanation:
Part A
First, we determine the scale factor from the map to the actual trail.
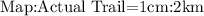
Next, we convert to same units:
![\begin{gathered} 1\operatorname{cm}\colon2\operatorname{km}=1\operatorname{cm}\colon2000m \\ =1\operatorname{cm}\colon200,000\operatorname{cm} \\ =1\colon200,000 \end{gathered}]()
The scale factor from the map to the actual trail is 1:200,000.
1 cm on the first map represents 2km on the actual trail.
The length of the trail on the first map = 8cm
Let the length of the actual trail = x
![\begin{gathered} \frac{1\operatorname{cm}}{2\operatorname{km}}=\frac{8\operatorname{cm}}{\text{x km}} \\ x=2*8=16\operatorname{km} \end{gathered}]()
The length of the actual trail is 16km.
Part B
The length of the trail on the first map = 8cm
The length of the trail on the second map = 6cm
The scale factor from the first map to the second map = 8:6 = 4:3
The dimensions of the triangle on the first map are 3mm, 4mm, and 5mm.
![\begin{gathered} (4)/(3)=(3)/(x) \\ 4x=9 \\ x=2.25\operatorname{mm} \end{gathered}]()
Similarly:
![\begin{gathered} (4)/(3)=(4)/(y) \\ 4y=12 \\ y=3\operatorname{mm} \end{gathered}]()
Finally:
![\begin{gathered} (4)/(3)=(5)/(z) \\ 4z=15 \\ z=3.75\operatorname{mm} \end{gathered}]()
The side lengths of the landmarks on the second map are 2.25mm, 3mm, and 3.75mm.