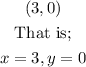Question

How is the system of linear equations determined, and how do we know if there is a solution?

Answer 1

Step-by-step explanation:

We are given three sets of systems of equations. To determine the description of each system, note that when a pair of lines intersect, the point at which they intersect has the coordinates that serve as the solution to that system of equations. For parallel lines which can NEVER intersect at any point, there is no solution. For lines that are the same regardless of how the equation is expressed, there are infinitely many solutions since they both will be satisfied by the same values at any given point.

Therefore, for the systems of equations given as A, B and C, we would have the following classification;

ANSWER:

`\begin{gathered} (A) \\ \text{This system of equations is INCONSISTENT} \\ There\text{ is no solution} \\ (B) \\ \text{This system of equations is CONSISTENT AND INDEPENDENT} \\ It\text{ has exactly one solution} \\ (C) \\ This\text{ system of equations is CONSISTENT AND DEPENDENT} \\ It\text{ has infinitely many solutions} \end{gathered}`

For system in graph B the solution is;

`\begin{gathered} (3,0) \\ \text{That is;} \\ x=3,y=0 \end{gathered}`