Given an equation below and evaluate the process:
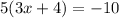
Step 1: Multiplication property of equality inorder to open the bracket
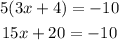
Step 2: Subtraction property of equality:
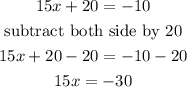
Step 3: Division property of equality:
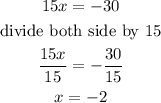
Step 4: Simplfying:

Therefore the correct value of x = -2