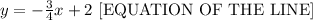Question

Find the equation of the line containing given point. Write the equation in slope-intercept form m= -3/4, point (8,-4)

Answer 1

Step-by-step explanation

Since we have the slope m=3/4 and the point (8,-4) we need to apply the slope intercept form of the line:

`y=mx+b`

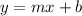
Where m=-3/4 and (x,y)=(8,-4)

Plugging in the terms into the equation:

`-4=\left(-(3)/(4)\right)*8+b`

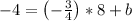
Multiplying numbers:

`-4=-6+b`

Adding +6 to both sides:

`-4+6=b`

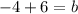
Subtracting numbers:

`2=b`

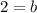
Plugging in b=2 into the equation:

`y=-(3)/(4)x+2\text{ \lbrack EQUATION OF THE LINE\rbrack}`