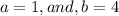Question

I need help, i keep seeing 3,-1 as the answer but i don’t have that option

Answer 1

Given the expression:

`x^2-2x-3=0`

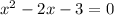
We will rewrite the expression to be as the form (x - a)² = b

So, we need to make a complete square

`x^2-2x=3`

The coefficient of x = -2

Half the coefficient = -1

Square it will give 1

So, add (1) to both sides of the equation

`x^2-2x+1=3+1`

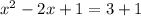
Factor the left side of the equation, it is a complete square

`(x-1)^2=4`

Compare the result to the given form.

So, the answer will be:

`a=1,and,b=4`