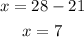Question

A mixture of 5% disinfectant solution is to be made from 8% and 4% disinfectant solutions. How much of each solution should be used if 28 gallons of 5% solution are needed?

Answer 1

You need 7 gallons of 8% solution and 21 gallons of 4% solution

Explanation

Data

• The concentration of solution 1: 8%

,

• The concentration of solution 2: 4%

Variables

• Amount of solution 1: x gallons

,

• Amount of solution 2: y gallons

The amount of disinfectant in solution 1 is 8% of the x gallons.

The amount of disinfectant in solution 2 is 4% of the y gallons.

The amount of disinfectant in the final mixture is 5% of the 28 gallons.

The final mixture is made by adding solution 1 to solution 2, that is,

`\begin{gathered} x+y=28\text{ \lparen total solution\rparen - eq. 1 } \\ x\cdot8\text{ \%}+y\cdot4\text{ \%}=28\cdot5\text{ \% \lparen amount of disinfectant\rparen} \\ 0.08x+0.04y=1.4\text{ \lparen changing percentage to decimals\rparen - eq. 2} \end{gathered}`

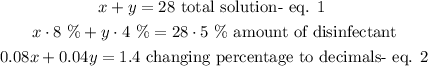
Isolating x from equation 1:

`x=28-y\text{ \lparen eq. 3\rparen}`

Substituting equation 3 into equation 2 and solving for y:

`\begin{gathered} 0.08(28-y)+0.04y=1.4 \\ 0.08(28)-0.08y+0.04y=1.4 \\ 2.24-0.04y=1.4 \\ -0.04y=1.4-2.24 \\ y=(-0.84)/(-0.04) \\ y=21 \end{gathered}`

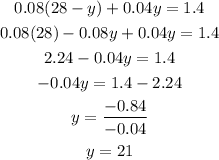
Substituting y = 21 into equation 3:

`\begin{gathered} x=28-21 \\ x=7 \end{gathered}`