Question

2. For each expression, write an equivalent expression by applyingthe distributive property.a. (x+2)(x+ 9)b. (x + 4)(2x - 1)c. (x - 5)

Answer 1

Accoding to the distributive property,

`(a+b)\ast(c+d)=a\ast(c+d)+b\ast(c+d)`

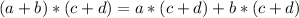
a.

Apply the property to the given expression,

`\begin{gathered} (x+2)(x+9) \\ =x\mleft(x+9\mright)+2\mleft(x+9\mright) \\ =x^2+9x+2x+18 \\ =x^2+11x+18 \end{gathered}`

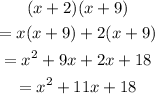
Thus, the given equivalent expression is,

`x^2+11x+18`

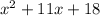
b.

Apply the property to the given expression,

`\begin{gathered} (x+4)(2x-1) \\ =x(2x-1)+2(2x-1) \\ =2x^2-x+4x-2 \\ =2x^2+3x-2 \end{gathered}`

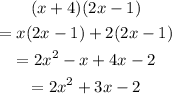
Thus, the given equivalent expression is,

`2x^2+3x+2`

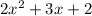
c.

To apply the Distributive Property, we need a 3rd term. But here are only two terms in the expression.

So the only other possible way to write the equation using Distributive property is given as,

`\begin{gathered} (x-5) \\ =1(x-5) \\ =1(x)-1(5) \end{gathered}`

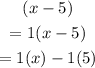
Thus, the required equivalent expression is ,

`1(x)-1(5)`