Question

Watch the video and then solve the problem given below.Click here to watch the video.Solve the inequality both algebraically and graphically. Give the solution in interval notation and draw it on a number line graph.x−32

Answer 1

Given the inequality

`(x-3)/(2)<(17)/(3)`

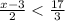
To solve the inequality algebraically

Crossmultiply to eliminate the denominators

`\begin{gathered} (x-3)/(2)<(17)/(3) \\ 3(x-3)<2*17 \\ 3x-9<34 \end{gathered}`

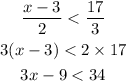
Collect like terms

`\begin{gathered} 3x-9<34 \\ 3x<34+9 \\ 3x<43 \\ \text{Divide both sides by 3} \\ (3x)/(3)<(43)/(3) \\ x<(43)/(3) \end{gathered}`

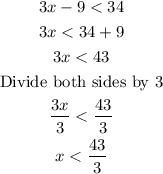
The graph of the given inequality is shown below

Hence, the interval notation of the given inequality is

`(-\infty,(43)/(3))`

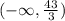
The number line of solution to the given inequality is shown below i.e (x < 43/3)