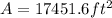
1) Since in that triangular lot, we only have the length of their legs. Then we can make use of Heron's formula to find the area:
![A=\sqrt[]{p(p-a)(p-b)(p-c)}](https://img.qammunity.org/2023/formulas/mathematics/college/trg9e1bc0wimtce49q6cqzpag6b1mug1ja.png)
3Note that, "p" stands for the Semiperimeter of that triangular lot, and "a", "b", and "c" make reference to each side length.
2) So let's calculate the Semiperimeter of that lot:
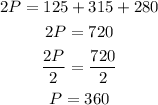
Now we can plug into Heron's formula:
![\begin{gathered} A=\sqrt[]{360(360-125)(360-315)(360-280)} \\ A=\sqrt[]{360(235)(45)(80)} \\ A=\sqrt[]{304560000} \\ A=17451.6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/u0vp2zx0hwnl3qf4wg3u1t8u6sp3mugoed.png)
And that is the answer (rounded off to the nearest tenth)